KMP (字符串模式匹配)

介绍

KMP 算法是一种改进的字符串匹配算法，由 D.E.Knuth，J.H.Morris 和 V.R.Pratt 提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称 KMP 算法）。KMP 算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个 next() 函数实现，函数本身包含了模式串的局部匹配信息。KMP 算法的时间复杂度 O(m+n)

问题

字符串 P 是否为字符串 S 的子串？如果是，它出现在 S 的哪些位置

• S 主串
• P 模式串

BF （暴力法）

最简单的想法就是从前往后逐个比较：

function BF(s, p) {
  let ls = s.length,
    lp = p.length;
  for (let i = 0; i <= ls - lp; ++i) {
    for (let j = 0; j < lp; ++j) {
      if (s[i + j] != p[j]) {
        break;
      } else if (j == lp - 1) return i;
    }
  }
}

记 S P 长度分别为 n m，时间复杂度就会是 O(m*n)

next 数组

定义： next[i] 表示 p(0,i) 这个子串的前 K 个字符串（前缀）和后 K 个字符串（后缀）相等

例 P=abcabd next[4]=2

P(0,4) = abcab 前面两个字符和后面两个相等

例

ababaabaabac
abaabac

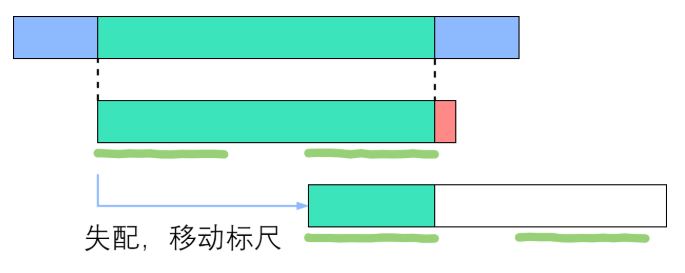
上面在 s[0] 开始匹配到 s[3] 匹配失败后，直接从 s[3] 开始接着匹配

因为 p(0,i) 子串中 前next[i]和后next[i] 字符一样，所以如果在p[r] 匹配失败，可以拿 next[r-1] 来作为前缀继续匹配

快速求 next 数组

function buildNext(p) {
  // 初始化 next[0]=0
  let next = [0];

  let x = 1,
    now = 0;
  while (x < p.length) {
    // 相等就向右扩展
    if (p[now] == p[x]) {
      now++;
      x++;
      next.push(now);
    } else if (now) {
      now = next[now - 1];
    } else {
      next.push(0);
      x++;
    }
  }
  return next;
}

完整代码

function buildNext(p) {
  // 初始化 next[0]=0
  let next = [0];

  let x = 1,
    now = 0;
  while (x < p.length) {
    // 相等就向右扩展
    if (p[now] == p[x]) {
      now++;
      x++;
      next.push(now);
    } else if (now) {
      now = next[now - 1];
    } else {
      next.push(0);
      x++;
    }
  }
  return next;
}

function search(s, p) {
  // tar 主串中的位置
  // pos 模式串中的位置
  let tar = (pos = 0);
  let next = buildNext(p);
  while (tar < s.length) {
    // 相等就都继续匹配
    if (s[tar] == p[pos]) {
      tar++;
      pos++;
    } else if (pos) {
      // 失败了如果pos!=0根据next移动
      pos = next[pos - 1];
    } else {
      // pos=0 失败了直接移动
      tar++;
    }
    // 匹配完成
    if (pos == p.length) {
      console.log(tar - pos + 1);
      pos = next[pos - 1];
    }
  }
}

版本 2

/**
 * @description: kmp 算法
 * @param {string} q 主串
 * @param {string} p 模式串
 * @return {type}
 */
function kmp(q, p) {
  let n = q.length,
    m = p.length;

  // 求 next 数组
  let next = new Array(m).fill(-1);
  for (let i = 1; i < m; ++i) {
    // 前面子串有几个重复的
    let j = next[i - 1];
    // 不相等就缩小范围
    while (j != -1 && p[j + 1] != p[i]) {
      j = next[j];
    }
    // 相等就加1
    if (p[j + 1] == p[i]) {
      next[i] = j + 1;
    }
  }

  // 模式串中的位置
  let match = -1;

  // 遍历主串
  for (let i = 0; i < n; ++i) {
    while (match != -1 && p[match + 1] != q[i]) {
      match = next[match];
    }
    if (p[match + 1] == q[i]) {
      ++match;
      if (match == m - 1) {
        return true;
      }
    }
  }
  return false;
}