# 抽稀 & 聚合

# 抽稀

概念

在处理矢量化数据时，记录中往往会有很多重复数据，对进一步数据处理带来诸多不便。多余的数据一方面浪费了较多的存储空间，另一方面造成所要表达的图形不光滑或不符合标准。因此要通过某种规则，在保证矢量曲线形状不变的情况下，最大限度地减少数据点个数，这个过程称为抽稀。

数据经过抽稀后，数量大量减少，并且基本保证能反映原图形或曲线的基本形状特征，能够为进一步的处理节省空间和时间。

抽稀在 GIS 矢量数据处理，图形数据压缩处理中有广泛的应用。

# 常见算法

步长法步长法是沿连续曲线每隔一定的步长抽取一点，其余点全部压缩掉，然后在相邻抽取点间用直线连续或曲线拟合逼近。这种方法主要有两点不足：一，曲线上的特征点，如曲线拐弯处，曲线变化较大的点可能因抽稀被压缩掉，导致曲线变形；二，在某些情况下，仍会留下部分多余点无法删除，如曲线中有一段比较直，而步长又较小，会导致此段直线上有多个抽取点，而实际上只要保留直线段的首尾点即可。因此，抽取后的曲线与原曲线有一定的误差，误差大小与步长的设置及曲线拟合方法有关。如果能综合考虑步长和曲率，可能会有更好的效果，但目前对步长和曲率没有明确的规定，一般是由编程人员根据实际情况自行决定。

线段过滤法线段过滤法是指当某一段的长度小于某一过滤值时，就以该段的中点代替该段，如同此段的两端退化到中点一样。线段过滤法同步长法一样，过滤值的大小决定着抽稀算法的精度，一般也是由编程人员自行确定。

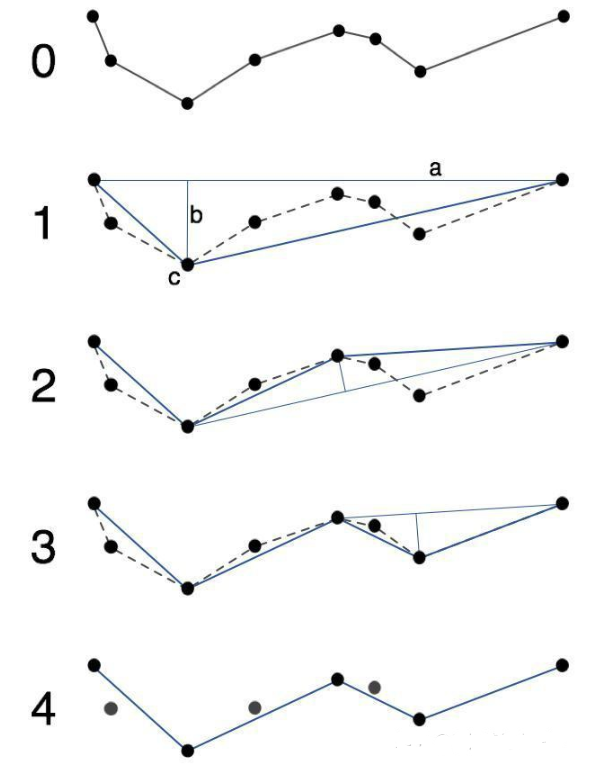
# 道格拉斯-普克（Douglas-Peuker)算法

leaflet 实现 (opens new window)

基本思路：

将待处理曲线的首末点虚连一条直线,求所有中间点与直线的距离,并找出最大距离值 dmax ,用 dmax 与抽稀阈值 threshold 相比较：
若 dmax < threshold，这条曲线上的中间点全部舍去;
若 dmax ≥ threshold，则以该点为界，把曲线分为两部分,对这两部分曲线重复上述过程，直至所有的点都被处理完成。

// 两个点距离的平方
function getSqDist(p1, p2) {
  var dx = p1.x - p2.x,
    dy = p1.y - p2.y;

  return dx * dx + dy * dy;
}

// 点到线段最大距离的平方
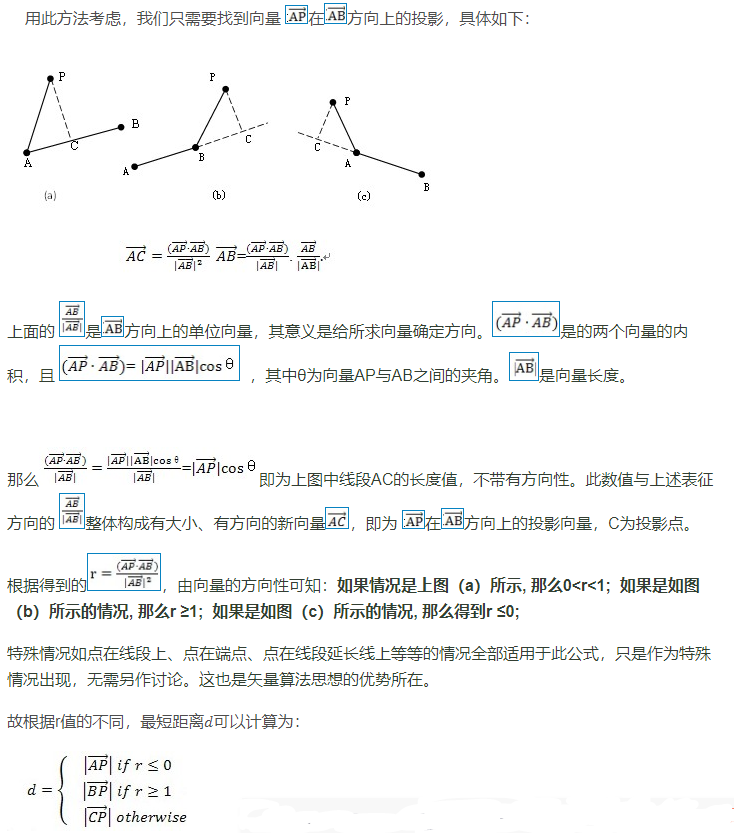
function getSqSegDist(p, p1, p2) {
  var x = p1.x,
    y = p1.y,
    dx = p2.x - x,
    dy = p2.y - y;

  if (dx !== 0 || dy !== 0) {
    var t = ((p.x - x) * dx + (p.y - y) * dy) / (dx * dx + dy * dy);

    if (t > 1) {
      x = p2.x;
      y = p2.y;
    } else if (t > 0) {
      x += dx * t;
      y += dy * t;
    }
  }

  dx = p.x - x;
  dy = p.y - y;

  return dx * dx + dy * dy;
}

// basic distance-based simplification
function simplifyRadialDist(points, sqTolerance) {
  var prevPoint = points[0],
    newPoints = [prevPoint],
    point;

  for (var i = 1, len = points.length; i < len; i++) {
    point = points[i];

    if (getSqDist(point, prevPoint) > sqTolerance) {
      newPoints.push(point);
      prevPoint = point;
    }
  }

  if (prevPoint !== point) newPoints.push(point);

  return newPoints;
}

function simplifyDPStep(points, first, last, sqTolerance, simplified) {
  var maxSqDist = sqTolerance,
    index;

  for (var i = first + 1; i < last; i++) {
    var sqDist = getSqSegDist(points[i], points[first], points[last]);

    if (sqDist > maxSqDist) {
      index = i;
      maxSqDist = sqDist;
    }
  }

  if (maxSqDist > sqTolerance) {
    if (index - first > 1)
      simplifyDPStep(points, first, index, sqTolerance, simplified);
    simplified.push(points[index]);
    if (last - index > 1)
      simplifyDPStep(points, index, last, sqTolerance, simplified);
  }
}

// simplification using Ramer-Douglas-Peucker algorithm
function simplifyDouglasPeucker(points, sqTolerance) {
  var last = points.length - 1;

  var simplified = [points[0]];
  simplifyDPStep(points, 0, last, sqTolerance, simplified);
  simplified.push(points[last]);

  return simplified;
}

// both algorithms combined for awesome performance
function simplify(points, tolerance, highestQuality) {
  if (points.length <= 2) return points;

  var sqTolerance = tolerance !== undefined ? tolerance * tolerance : 1;

  points = highestQuality ? points : simplifyRadialDist(points, sqTolerance);
  points = simplifyDouglasPeucker(points, sqTolerance);

  return points;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

在线示例 (opens new window)

← GIS